【23xiu.com-爱上秀-教育信息门户网】
几何综合问题常常因其图形变化多端,方法多种多样而被命题老师所青睐,成为近几年中考数学的热点。
中考数学题目每年看上去千变万化,但万变不离其宗,题目在变,但题型不变。如每一道中考几何题目背后都有着一定的法规律,每一类题型都有着相似的解题思想,这种思想的集中体现,便是解题思路和方法。
只有抓住解题思路和方法,我们才能从容应对几何综合问题,但要熟练掌握几何综合问题的解题思想和方法并非一朝一夕,需要我们在大量的解题,同时不断去总结方法,这样最终才能培养出来。
如几何综合问题常常以数与形、代数计算与几何证明、相似三角形的判定与性质、画图分析与列方程求解、勾股定理与函数、圆和三角相结合的综合性试题出现。同时会考查到一些数学思想:如数形结合思想、分类讨论思想、几何运动变化等数学思想。
典型例题1:
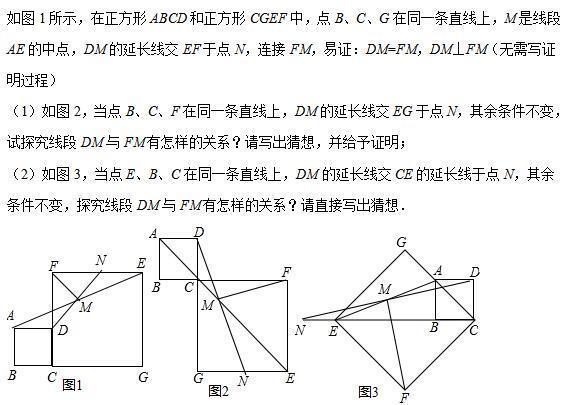


考点分析:
四边形综合题.
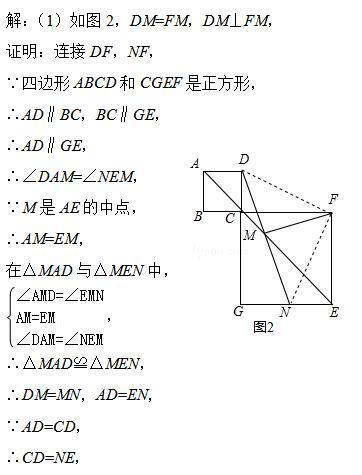
题干分析: (1)连接DF,NF,由四边形ABCD和CGEF是正方形,得到AD∥BC,BC∥GE,于是得到AD∥GE,求得∠DAM=∠NEM,证得△MAD≌△MEN,得出DM=MN,AD=EN,推出△MAD≌△MEN,证出△DFN是等腰直角三角形,即可得到结论;
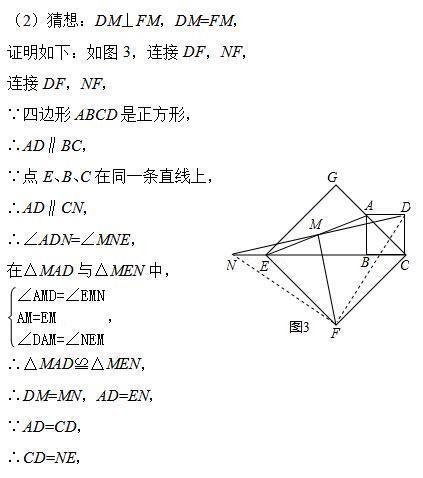
(2)连接DF,NF,由四边形ABCD是正方形,得到AD∥BC,由点E、B、C在同一条直线上,于是得到AD∥CN,求得∠DAM=∠NEM,证得△MAD≌△MEN,得出DM=MN,AD=EN,推出△MAD≌△MEN,证出△DFN是等腰直角三角形,于是结论得到.
解题反思:
本题考查了全等三角形的判定,正方形的性质,等腰直角三角形的判定和性质,本题中的难点是辅助线的作法,作好辅助线找对解题的方向是本题解答的关键所在。
几何综合问题因其能很好体现数学逻辑关系,考查考生思维能力,因此几何综合问题是中考数学常考题型,在中考数学中仍占有相当的比例。
对于几何综合问题解题思想方法的总结,分为很多层面,最基本的形似,看到相仿的图形相仿或相似的题目,能够有意识的联想以前学过的题型并加以运用和套用。
数学学习不要死做题,要学会通过解题来收集、整理、归纳各类方法,并形成体系,凸显解题规律和数学思想。