【23xiu.com-爱上秀-教育信息门户网】
“为什么每次考试感觉都很好,成绩却很一般?”
“为什么感觉题目都做过,就是做不起来?”
“明明方法都是对的,为什么就是算不出正确答案?”
在数学学习过程中,很多学生面对一道题目,总感觉自己都是对的,无论是过程还是计算,但为什么结果都是错的?有些学生算到最后,都怀疑自己是不是适合学习数学。
对于数学学习,其实我们一定要明白一个道理:懂了≠会做≠做对。
掌握数学知识不仅要去记忆,更需要我们通过一定量的习题训练,才能最终掌握这些数学知识。在这里我们一定要明白一个道理,那就是数学不是题做得越多,分数就越高。提高数学成绩需要合适的学习策略、恰当的学习方法,加上一定题目训练,才能让数学成绩显著提高。如首先要熟练掌握书本上所有基础知识内容,并学会运用,同时更要学会运用数学思想来解决问题。

因此,一个人如果仅仅是知道知识点,但不会运用知识去解决问题,就是相当于懂了,但不会做。学习知识点的最终目的是要转化为数学能力,把该知识点所相关的数学思想和方法好好掌握,渐渐通过解数学题把具体知识点转化为学习能力。
做数学题一定要充分理解题意,注意对整个问题的提炼,深化对题中某个条件的认识;看看与哪些数学基础知识相联系,有没有出现一些新的功能或用途?再现思维活动经过,分析想法的产生及错因的由来,要求用口语化的语言真实地叙述自己的做题经过和感想,想到什么就写什么,以便挖掘出一般的数学思想方法和数学思维方法;一题多解,一题多变,多元归一。
典型例题1:
综合与探究
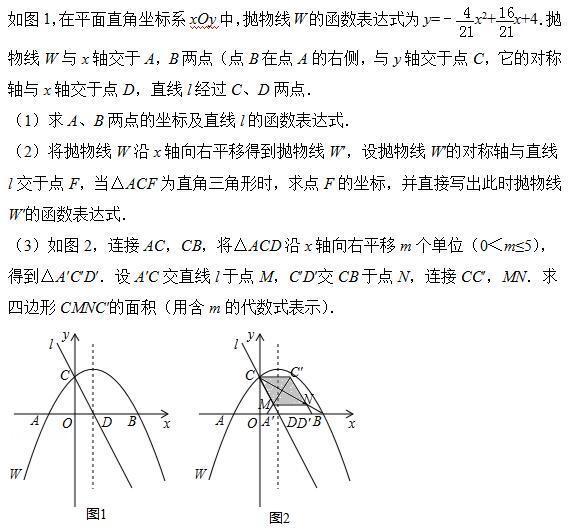
题干分析:
(1)根据自变量与函数值对应关系,当函数值为零时,可得A、B点坐标,当自变量为零时,可得C点坐标,根据对称轴公式,可得D点坐标,根据待定系数法,可得l的解析式;
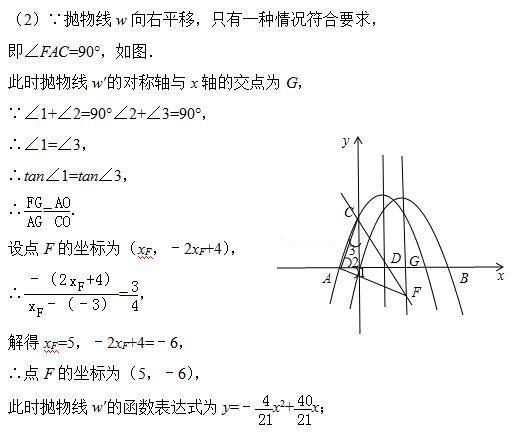
(2)根据余角性质,可得∠1与∠3的关系,根据正切的定义,可得关于F点的横坐标的方程,根据解方程,可得F点坐标,平移后的对称轴,根据平移后的对称轴,可得平移后的函数解析式;
(3)根据图象平移的规律,可得A′,C′,D′′点的坐标,根据待定系数法,可得A′C,BC,C′D′的解析式,根据解方程组,可得M、N的坐标,根据平行四边形的判定,可得四边形CMNC′的形状,根据平行四边形的面积公式,可得答案.


考点分析:
二次函数综合题。
解题反思:
本题考察了二次函数综合题,(1)利用了自变量与函数值的对应关系,待定系数法求函数解析式;(2)利用了余角的性质,正切函数的性质,利用等角的正切函数值相等得出关于F点横坐标的方程是解题关键;(3)利用了图象的平移规律,待定系数法求函数解析式,解方程组得出M、N的坐标是解题关键,又利用了平行四边形的判定,平行四边形的面积公式。
很多学生知识点都懂,方法也知道,但计算能力非常薄弱,一道大题可能从第一步就算错,不管你之后写的多漂亮,过程多完美,但整个计算过程都出错,怎么可能拿到满分呢?一个人的计算能力是学好数学的基本功,小学到初中是培养我们数学计算能力的黄金时期,如有理数的运算、整数的运算、因式分解、分式的运算、根式的运算和解方程等等。

掌握数学知识点不难,但学会运用数学知识点比较难难。解数学题是数学学习的重要环节,但很多人学习数学只知道做题、刷题,从不讲究方法,这样当然提分难。数学成绩上不去,我们一定要尽快分析。
大家一定要清楚的知道自己薄弱知识点环节在哪里。针对自己的薄弱环节进行题型训练。数学学习,我们不能一味跳进题海,期望“刷题”、“以多取胜”,往往这种方法到头来常常是事倍功半。
数学的解题思路,就是在训练中训练出来的。我们要学会通过对以往题目的总结,得出一些解题思路。如一些定理、数学思想的运用,然后再结合一些针对性习题加以训练,就能在一定时间内取得进步。