【23xiu.com-爱上秀-教育信息门户网】
随着教师考试临近,想必许多考生都在为没有合适的示范教案而烦恼,常常困扰于课程内容太多无法删减,时间自然也无法保障。本文以数学学科《变量与函数》为例,为您呈现10-20分钟的课堂教案,精简的速写教案将成为您备考的参考依据。

一、教学目标
知识与技能目标:借助简单实例,学生初步感知用常量与变量来刻画一些简单的数学问题,能指出具体问题中的常量、变量.初步理解存在一类变量可以用函数方式来刻画,能举出涉及两个变量的实例,并指出由哪一个变量确定另一个变量,这两个变量是否具有函数关系.初步理解对应的思想,体会函数概念的核心是两个变量之间的特殊对应关系,能判断两个变量间是否具有函数关系.
过程与方法目标:借助简单实例,引领学生参与变量的发现和函数概念的形成过程,体会从生活实例抽象出数学知识的方法,感知现实世界中变量之间联系的复杂性,数学研究从最简单的情形入手,化繁为简.
情感态度与价值观目标:从学生熟悉、感兴趣的实例引入课题,引领学生参与变量的发现和函数概念的形成过程,体验“发现、创造”数学知识的乐趣.学生初步感知实际生活蕴藏着丰富的数学知识,感知数学是有用、有趣的学科.
二、教学重难点
重点:借助简单实例,从两个变量间的特殊对应关系抽象出函数的概念.
难点:怎样理解“唯一对应”.
三、教学过程
(一)导言:
1.《名侦探柯南》中有这样一个情景:柯南根据案发现场的脚印,锁定疑犯的身高.你知道其中的道理吗?
2.我们班中同学A与职业相扑运动员,谁的饭量大?你能说明理由吗?
问题1中都涉及两个量的关系,脚印确定,对应的身高有多个取值;问题2涉及多个量的关系.这一节课我们研究两个量的关系,研究怎样由一个量来确定另一个量.
(二)概念的引入
1.票房收入问题:每张电影票的售价为10元.
(1)若一场售出150张电影票,则该场的票房收入___________元;若售出205张、310张呢?
(2)若一场售出x张电影票,则该场的票房收入y元,则y=__________.
思考:
(1)票房收入随售出的电影票变化而变化,即y随________的变化而变化;
(2)当售出票数x取定一个确定的值时,对应的票房收入y的取值是否唯一确定?
2.成绩问题:如图是某班同学一次数学测试中的成绩登记表:这一次数学测试中,13号的成绩为______;15号的成绩为______;16号的成绩为______;23号的成绩为______.
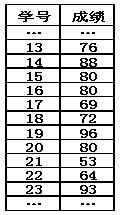
思考:
(1)测试成绩随________的变化而变化;
(2)任意确定一个学号x,对应的成绩f的取值是否唯一确定?
3.气温问题:图一是抚顺春季某一天的气温T随时间t变化的图象,看图回答:
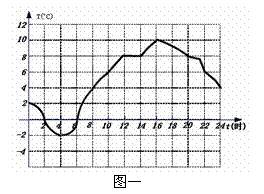
(1)这天的8时的气温是_________℃,14时的气温是_______℃,最高气温是________℃,最低气温是______℃;
(3)这一天中,在4时~12时,气温( ),在16时~24时,气温( ).
A.持续升高 B.持续降低 C.持续不变
思考:
(1)天气温度随_____________的变化而变化,即T随______________的变化而变化;
(2)当时间t取定一个确定的值时,对应的温度T的取值是否唯一确定?
(三)概念的界定
思考:上述三个问题中,分别涉及哪些量的关系?通过哪一个量可以确定另一个量?
在上面的三个问题中,其中一个量的变化引起另一个量的变化(按照某种规律变化),变化的量叫做变量;有些量的值始终不变(例如电影票的单价10元……).并且当其中一个变量取定一个值时,另一个变量就随之确定,且它的对应值只有一个.
教师根据学生的回答,在黑板上板书:
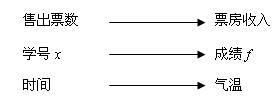
师生对上述三个问题进行分析,找出它们的共性,归纳出函数的概念
【设计意图】(1)如何把具体的实例进行抽象,形式化为数学知识是本课的关键.这里提出的问题“上述三个问题中,分别涉及哪些量的关系?通过哪一个量可以确定另一个量?”是一个关键的“脚手架”,借助“脚手架”,学生经历数学概念的形成过程,引导学生认识为什么要引进变量、常量、函数的概念,逐步了解如何给数学概念下定义.(2)此处板书是“脚手架”的重要组成部分,揭示“两个量的对应关系”.
问题回顾:指出前面三个问题中涉及到的量,并指出其中的变量、常量、自变量与函数.
例1 一个三角形的底边为5,这一边上的高h可以任意伸缩.
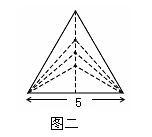
(1)高h的变化会引起三角形中哪些量发生变化?这些变量是高h的函数吗?
(2)试求面积s随h变化的关系式,并指出其中的常量、变量与自变量。
例2如果用r表示圆的半径,半径r的变化会引起圆中哪些量发生变化?这些变量是半径r的函数吗?
例3问题1中,售出票数是票房的函数吗?问题2中,学号x是成绩f的函数吗?
(四)概念巩固
1.购买一些签字笔,单价3元,总价为y元,签字笔为x支,根据题意填表:
(1)y随x变化的关系式y =______________,______ 是自变量,______ 是______ 的函数;
(2)当购买8支签字笔时,总价为______元.
2.周末,小李8时骑自行车从家里出发,到野外郊游,16时回到家里.他离开家后的距离s(千米)与时间t(时)的关系如图所示.
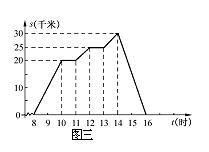
(1)当t=12时,s=________;当t=14时,s=________;
(2)小李从______时开始第一次休息,休息时间为____小时,此时离家______千米.
(3)距离s是时间t的函数吗?时间t是距离s的函数吗?
【设计意图】(1)例题和巩固练习,巩固变量与函数等概念,让学生充分体会到许多问题中的变量关系都存在着函数关系,隐含着在函数关系中表示两个变量的对应关系有解析法、列表法、图象法.(2)练习二2(4)从逆向思维的角度提出具有实际背景的问题有利于学生理解函数的“单值对应关系”,有利于学生明确“由哪一个量能唯一确定另一个量”,让学生养成多角度思考的习惯.
(五)概念辨析
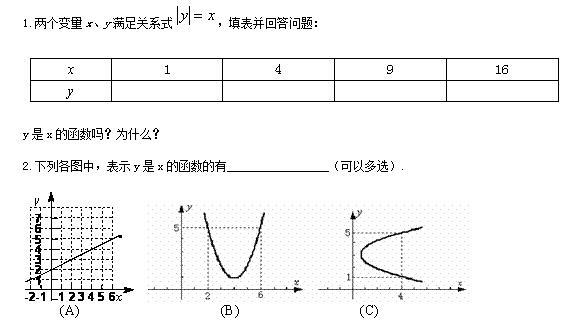
3.你能举出涉及两个变量的例子吗?它们具有函数关系吗?
【设计意图】理解函数概念的核心是“①由哪一个变量确定另一个变量;②唯一对应关系”,给定自变量x的任意一个值就有唯一确定的y的值和它对应,这样的对应可以是“自变量的一个取值对应因变量的一个取值”(简称“一对一”),也可以是“自变量的多个取值对应因变量的同一个取值”(简称“多对一”),但不可以是“自变量的同一个取值对应因变量的多个取值”(简称“一对多”).
(六)质疑、小结
1.这一节课你有什么收获?还有什么疑问?你可以编一道题考一考同学,也可以向同学请教.
2.函数是一种“数”吗?
【设计意图】通过小结,让学生抓住函数概念的实质.