【23xiu.com-爱上秀-教育信息门户网】
归纳猜想类问题也是探索规律型问题,这类问题一般给出一组具有某种有规律的数、式、图形,或是给出与图形有关的操作变化过程,或某一具体的问题情境,通过认真观察、分析推理,探究其中蕴含的规律,进而归纳或猜想出一般性的结论。考查学生的归纳、概括、类比能力。有利于培养学生思维的深刻性和创造性。
解决归纳猜想类问题的基本思路是“观察→归纳→猜想→证明(验证)”,具体做法:
1、认真观察所给的一组数、式、图等,发现它们之间的关系;
2、根据它们之间的关系分析、概括,归纳它们的共性和蕴含的变化规律,猜想得出一个一般性的结论;
3、结合题目所给的材料情景证明或验证结论的正确性。
典型例题1:


解题反思:
本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线,直线上任意一点的坐标都满足函数关系式y=kx+b。也考查了等腰直角三角形的性质。
归纳猜想类问题可以分成四大类:
一、数式归纳猜想题
这类题通常是先给出一组数或式子,通过观察、归纳这组数或式子的共性规律,写出一个一般性的结论。找出题目中规律,即不变的和变化的,变化的部分与序号的关系是解这类题的关键。
二、图形归纳猜想题
此类题通常给出一组图形的排列(或操作得到一系列的图形)探求图形的变化规律,以图形为载体考查图形所蕴含的数量关系。其解题关键是找出相邻两个图形之间的位置关系和数量关系。
典型例题2:


解题反思:
此题考查了一次函数函数图象上点的坐标特点,先根据题意得出T点纵坐标变化规律进而得出S的变化规律,得出图形面积变化规律是解题关键。
三、结论归纳猜想题
结论归纳猜想题常考数值结果、数量关系及变化情况。发现或归纳出周期性或规律性变化,是解题的关键。
典型例题3:
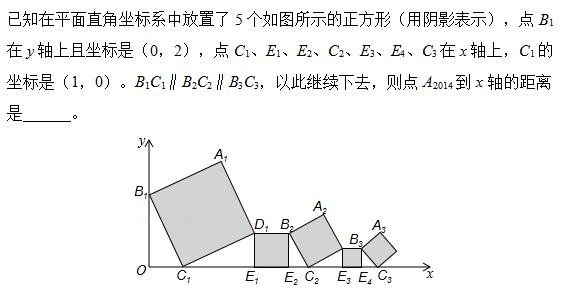

解题反思:
此题主要考查了正方形的性质以及解直角三角形的知识,得出正方形各边长是解题关键。
四、类比归纳猜想题
类比归纳猜想题通常是指由两类对象的具有某些相同或相似的性质,和其中一类对象的某些已知的性质,推断出另一类对象也具有这些性质的一种题型,有时也指两个对象在研究方法、学习过程上类比,考查类比归纳推理能力。