【23xiu.com-爱上秀-教育信息门户网】
一个人的空间想象能力主要是指对客观事物的空间形式进行观察、分析、抽象思考和创新的能力。
说得简单点,空间想象能力是对空间图形处理的能力。
高考数学的《考试大纲》对学生的空间想象能力提出以下要求:
能根据条件作出正确的图形,根据图形想象出直观形象;
能正确的分析出图形中的基本元素及相互关系;
能对图形进行分解,组合与变换;
会运用图形与图表等手段形象的揭示问题的本质。

在高考数学中考查空间想象能力主要是通过立体几何内容考查,立体几何中立体图形的特征是通过概念描述的,而对图形的理解是解题的基础。
培养和发展学生的空间想象能力是立体几何教学中的重点,也是教学中的难点。因此,今天我们就一起结合实际例题来讲讲如何培养学生的空间想象能力。
空间想象能力是对空间形式的观察、分析、抽象的能力,主要表现为识图,画图和对图形的想象能力。识图是指观察、研究所给图形中几何元素之间的相互关系;画图是指将文字语言和符号语言转化为图形语言,以及对图形添加辅助图形或对图形进行各种变换;对图形的想象主要包括有图想图和无图想图两种,是空间想象能力高层次的标志。
典型例题1:
如图1所示,在Rt△ABC中,AC=6,BC=3,∠ABC=90°,CD为∠ACB的角平分线,点E在线段AC上,CE=4.如图2所示,将△BCD沿CD折起,使得平面BCD⊥平面ACD,连接AB,设点F是AB的中点.
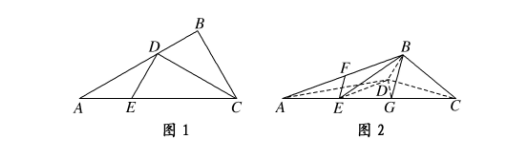
(1)求证:DE⊥平面BCD;
(2)若EF∥平面BDG,其中G为直线AC与平面BDG的交点,求三棱锥B-DEG的体积.
解:(1)证明:∵AC=6,BC=3,∠ABC=90°,
∴∠ACB=60°.
∵CD为∠ACB的角平分线,∴∠BCD=∠ACD=30°.
∴CD=2.
∵CE=4,∠DCE=30°,
∴DE=2.
则CD2+DE2=EC2.
∴∠CDE=90°,DE⊥DC.
又∵平面BCD⊥平面ACD,平面BCD∩平面ACD=CD,DE⊂平面ACD,
∴DE⊥平面BCD.
(2)∵EF∥平面BDG,EF⊂平面ABC,平面ABC∩平面BDG=BG,
∴EF∥BG.
∵点E在线段AC上,CE=4,点F是AB的中点,
∴AE=EG=CG=2.
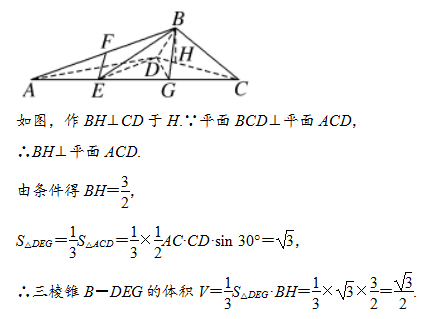
在高考数学中考查学生的空间想象能力,基本题型都会要求学生根据题设条件想象和画出图形。如在考题中,一般只给出最简单的图形及最基本条件,在解答时需要以此为依托,根据定义和性质自己画出所需的线、面。
对图形处理的另一方面就是分割、补形、折叠、展平,通过对图形的这些直观处理一般能辅助解题,使解题过程简捷、明快。在图形中确定元素间的基本位置关系要求考生能结合图形进行一定的论证。

我们翻阅历年高考数学中有关立体几何的题目,不难发现命题紧扣要求,从各层面、各角度进行考查,既有基础知识的落实,更有能力的体现。
典型例题2:
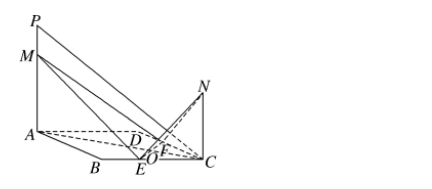
如图,已知E,F分别是正方形ABCD边BC,CD的中点,EF与AC交于点O,PA,NC都垂直于平面ABCD,且PA=AB=4,NC=2,M是线段PA上的一动点.
(1)求证:平面PAC⊥平面NEF;
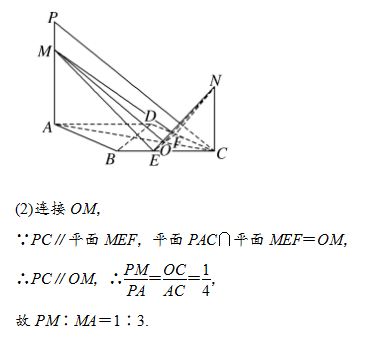
(2)若PC∥平面MEF,试求PM∶MA的值.
解:(1)证明:连接BD,
∵PA⊥平面ABCD,
BD⊂平面ABCD,
∴PA⊥BD.
又∵BD⊥AC,AC∩PA=A,
∴BD⊥平面PAC.
又∵E,F分别是BC,CD的中点,
∴EF∥BD.
∴EF⊥平面PAC,
又EF⊂平面NEF,
∴平面PAC⊥平面NEF.
立体图形画在平面必然与实际图形产生差异,容易造成错觉,正确认识各元素的空间位置和图形的空间结构;空间想象能力的第二层次表现为能准确领会“点线—线线—线面-—面面”之间的联系,并能就解题的根据、需要,对这些关系加以转化,多数情况是把给出的条件转化到某个平面上来,利用平面几何的知识来解题;空间想象能力的第三个层次,是能对题中给出的图形进行分割一分解,组合一拼补,变形一转换、位移或从不同视角观察图形,从而寻找出解题的最佳方法。