【23xiu.com-爱上秀-教育信息门户网】
不等式这一块知识内容能很好体现高中数学的综合性、灵活多样性,能充分培养学生逻辑推理论证的能力、分析问题解决问题的能力,渗透在数学各个知识板块中,同时能考查考生对数学各部分知识融会贯通的掌握情况。因此,不等式这部分知识在高考数学占有一定比重,有着十分广泛的应用。
今天我们就来讲讲怎么应对高考数学中不等式的内容。
使用不等式性质时应注意的问题:
在使用不等式时,一定要搞清它们成立的前提条件.不可强化或弱化成立的条件.如“同向不等式”才可相加,“同向且两边同正的不等式”才可相乘;可乘性中“c的符号”等也需要注意。
作差法是比较两数(式)大小的常用方法,也是证明不等式的基本方法.要注意强化化归意识,同时注意函数性质在比较大小中的作用。
典型例题1:
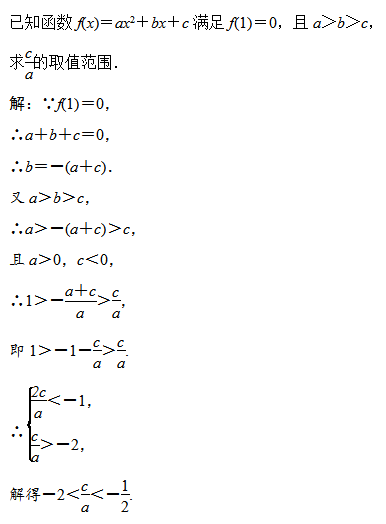
比较大小的常用方法
(1)作差法:
一般步骤是:①作差;②变形;③定号;④结论.其中关键是变形,常采用配方、因式分解、有理化等方法把差式变成积式或者完全平方式.当两个式子都为正数时,有时也可以先平方再作差.
(2)作商法:
一般步骤是:①作商;②变形;③判断商与1的大小;④结论.
(3)特值法:
若是选择题、填空题可以用特值法比较大小;若是解答题,可先用特值探究思路,再用作差或作商法判断.
在解决不等式综合问题时候,经常需要结合其他知识内容,如集合问题、方程(组)的解的讨论、函数单调性的研究、函数定义域的确定、三角、数列、复数、立体几何、解析几何中的最大值、最小值问题等等,无一不与不等式有着密切的联系,许多问题,最终都可归结为不等式的求解或证明。
典型例题2;
某企业去年年底给全部的800名员工共发放2 000万元年终奖,该企业计划从今年起,10年内每年发放的年终奖都比上一年增加60万元,企业员工每年净增a人.
(1)若a=10,在计划时间内,该企业的人均年终奖是否会超过3万元?
(2)为使人均年终奖年年有增长,该企业每年员工的净增量不能超过多少人?

判断一个关于不等式的命题的真假时,先把要判断的命题与不等式性质联系起来考虑,找到与命题相近的性质,并应用性质判断命题的真假,当然判断的同时可能还要用到其他知识,比如对数函数、指数函数的性质。
特殊值法是判断命题真假时常用到的一个方法,在命题真假未定时,先用特殊值试试,可以得到一些对命题的感性认识,如正好找到一组特殊值使命题不成立,则该命题为假命题。